Boost.Graphに入門

k.inabaさんおすすめの『最短経路の本』でグラフ理論の勉強中。

簡単なグラフを用意して、

Boost.Graphで最短経路の計算。

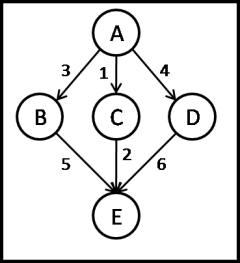
#include <iostream>
#include <vector>
#include <string>
#include <boost/graph/graph_traits.hpp>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <boost/graph/graph_utility.hpp>
#include <boost/spirit/home/phoenix/algorithm.hpp>

using namespace boost;

typedef adjacency_list<listS, vecS, directedS,
    no_property, property<edge_weight_t, int> > Graph;
typedef std::pair<int, int>                     Edge;
typedef graph_traits<Graph>::vertex_descriptor  Vertex;

enum { A, B, C, D, E, N };
const std::string name = "ABCDE";
const int vertex_count = N;

int main()
{
    // 辺
    std::vector<Edge> edges = {
        {A, B}, {A, C}, {A, D},
        {B, E}, {C, E}, {D, E}
    };

    // 距離
    std::vector<int> weights = {
        3, 1, 4,
        5, 2, 6
    };

    // グラフ作成
    Graph g(edges.begin(), edges.end(), weights.begin(), vertex_count);

    // 最短経路を計算
    std::vector<Vertex> p(num_vertices(g));
    dijkstra_shortest_paths(g, A,
        visitor(make_dijkstra_visitor(record_predecessors(&p[0], on_edge_relaxed()))));

    // 結果を表示
    adjacency_list<> tree(vertex_count);
    boost::phoenix::for_each(vertices(g), [&](const graph_traits<Graph>::vertex_descriptor& v) {
        if (v != p[v])
            add_edge(p[v], v, tree);
    })();
    print_graph(tree, name.c_str());
}

A --> B C D
B -->
C --> E
D -->
E -->

結果の見方がよくわからないけど、A -> C -> Eが最短経路、ということでいいのかな。

最長経路も計算してみようかな、と思って距離に-1を掛けたら、
dijkstra_shortest_pathsの計算でboost::negative_edge例外が投げられた。
dijkstraでは負のweightはダメらしい( http://twitter.com/yuyarin/statuses/12079231528 )

#include <iostream>
#include <vector>
#include <string>
#include <boost/graph/graph_traits.hpp>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <boost/graph/graph_utility.hpp>
#include <boost/lambda/lambda.hpp>
#include <boost/spirit/home/phoenix/algorithm.hpp>

using namespace boost;
using boost::lambda::_1;

typedef adjacency_list<listS, vecS, directedS,
    no_property, property<edge_weight_t, int> > Graph;
typedef std::pair<int, int>                     Edge;
typedef graph_traits<Graph>::vertex_descriptor  Vertex;

enum { A, B, C, D, E, N };
const std::string name = "ABCDE";
const int vertex_count = N;

int main()
{
    // 辺
    std::vector<Edge> edges = {
        {A, B}, {A, C}, {A, D},
        {B, E}, {C, E}, {D, E}
    };

    // 距離
    std::vector<int> weights = {
        3, 1, 4,
        5, 2, 6
    };
    std::transform(weights.begin(), weights.end(), weights.begin(), _1 * -1);

    // グラフ作成
    Graph g(edges.begin(), edges.end(), weights.begin(), vertex_count);

    // 最短経路を計算
    std::vector<Vertex> p(num_vertices(g));
    dijkstra_shortest_paths(g, A,
        visitor(make_dijkstra_visitor(record_predecessors(&p[0], on_edge_relaxed()))));
        // throw boost::negative_edge

    // 結果を表示
    adjacency_list<> tree(vertex_count);
    boost::phoenix::for_each(vertices(g), [&](const graph_traits<Graph>::vertex_descriptor& v) {
        if (v != p[v])
            add_edge(p[v], v, tree);
    })();
    print_graph(tree, name.c_str());
}

bellman_ford_shortest_pathsなら負のweightも扱えるらしい( http://twitter.com/yuyarin/statuses/12079292134 )のでやってみた。
まず最短経路。

#include <iostream>
#include <vector>
#include <string>
#include <numeric>
#include <boost/graph/graph_traits.hpp>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/bellman_ford_shortest_paths.hpp>
#include <boost/graph/graph_utility.hpp>
#include <boost/spirit/home/phoenix/algorithm.hpp>

using namespace boost;

typedef adjacency_list<listS, vecS, directedS,
    no_property, property<edge_weight_t, int> > Graph;
typedef std::pair<int, int>                     Edge;
typedef graph_traits<Graph>::vertex_descriptor  Vertex;

enum { A, B, C, D, E, N };
const std::string name = "ABCDE";
const int vertex_count = N;

int main()
{
    // 辺
    std::vector<Edge> edges = {
        {A, B}, {A, C}, {A, D},
        {B, E}, {C, E}, {D, E}
    };

    // 距離
    std::vector<int> weights = {
        3, 1, 4,
        5, 2, 6
    };

    // グラフ作成
    Graph g(edges.begin(), edges.end(), weights.begin(), vertex_count);

    // 最短経路を計算
    property_map<Graph, edge_weight_t>::type weight_pmap = get(edge_weight, g);
    std::vector<int> distance(vertex_count, std::numeric_limits<short>::max());

    std::vector<std::size_t> parent(vertex_count);
    std::iota(parent.begin(), parent.end(), 0);

    bellman_ford_shortest_paths(g, vertex_count,
        weight_map(weight_pmap).distance_map(&distance[0]).
        predecessor_map(&parent[0]).root_vertex(A));

    // 結果を表示
    adjacency_list<> tree(vertex_count);
    boost::phoenix::for_each(vertices(g), [&](const graph_traits<Graph>::vertex_descriptor& v) {
        if (v != parent[v])
            add_edge(parent[v], v, tree);

    })();

    print_graph(tree, name.c_str());
}

A --> B C D
B -->
C --> E
D -->
E -->

結果はさっきと同じ。
次に最長経路。

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <numeric>
#include <boost/graph/graph_traits.hpp>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/bellman_ford_shortest_paths.hpp>
#include <boost/graph/graph_utility.hpp>
#include <boost/lambda/lambda.hpp>
#include <boost/spirit/home/phoenix/algorithm.hpp>

using namespace boost;
using boost::lambda::_1;

typedef adjacency_list<listS, vecS, directedS,
    no_property, property<edge_weight_t, int> > Graph;
typedef std::pair<int, int>                     Edge;
typedef graph_traits<Graph>::vertex_descriptor  Vertex;

enum { A, B, C, D, E, N };
const std::string name = "ABCDE";
const int vertex_count = N;

int main()
{
    // 辺
    std::vector<Edge> edges = {
        {A, B}, {A, C}, {A, D},
        {B, E}, {C, E}, {D, E}
    };

    // 距離
    std::vector<int> weights = {
        3, 1, 4,
        5, 2, 6
    };

    // 距離に-1を掛けると最短距離の計算が最長距離の計算になる
    std::transform(weights.begin(), weights.end(), weights.begin(), _1 * -1);

    // グラフ作成
    Graph g(edges.begin(), edges.end(), weights.begin(), vertex_count);

    // 最短経路を計算
    property_map<Graph, edge_weight_t>::type weight_pmap = get(edge_weight, g);
    std::vector<int> distance(vertex_count, std::numeric_limits<short>::max());

    std::vector<std::size_t> parent(vertex_count);
    std::iota(parent.begin(), parent.end(), 0);

    bellman_ford_shortest_paths(g, vertex_count,
        weight_map(weight_pmap).distance_map(&distance[0]).
        predecessor_map(&parent[0]).root_vertex(A));

    // 結果を表示
    adjacency_list<> tree(vertex_count);
    boost::phoenix::for_each(vertices(g), [&](const graph_traits<Graph>::vertex_descriptor& v) {
        if (v != parent[v])
            add_edge(parent[v], v, tree);

    })();

    print_graph(tree, name.c_str());
}

A --> B C D
B -->
C -->
D --> E
E -->

「A -> D -> E」
合ってるっぽい。

んー、Boost.Graphむずかしっ。